An Example of Intrinsic Motivation Is Reading a Textbook Because
Statistical Thinking
Past and Allan RossmanCalifornia Polytechnic Country University, San Luis Obispo
Every bit our club increasingly calls for evidence-based decision making, information technology is important to consider how and when we can draw valid inferences from data. This module volition use four recent research studies to highlight central elements of a statistical investigation.
Learning Objectives
- Define basic elements of a statistical investigation.
- Describe the function of p-values and confidence intervals in statistical inference.
- Describe the office of random sampling in generalizing conclusions from a sample to a population.
- Describe the function of random consignment in drawing cause-and-effect conclusions.
- Critique statistical studies.
Introduction
Does drinking coffee actually increase your life expectancy? A recent study (Freedman, Park, Abnet, Hollenbeck, & Sinha, 2012) institute that men who drank at least six cups of coffee a twenty-four hours had a 10% lower take a chance of dying (women xv% lower) than those who drank none. Does this hateful you should pick up or increase your own coffee habit?
Modern society has become awash in studies such as this; yous tin can read about several such studies in the news every 24-hour interval. Moreover, data abound everywhere in modern life. Conducting such a study well, and interpreting the results of such studies well for making informed decisions or setting policies, requires understanding bones ideas of statistics, the science of gaining insight from data. Rather than relying on chestnut and intuition, statistics allows us to systematically study phenomena of involvement.

Key components to a statistical investigation are:
- Planning the study: Offset by asking a testable research question and deciding how to collect information. For case, how long was the report period of the coffee written report? How many people were recruited for the study, how were they recruited, and from where? How sometime were they? What other variables were recorded nearly the individuals, such every bit smoking habits, on the comprehensive lifestyle questionnaires? Were changes made to the participants' coffee habits during the course of the study?
- Examining the data: What are appropriate ways to examine the data? What graphs are relevant, and what do they reveal? What descriptive statistics can be calculated to summarize relevant aspects of the data, and what practice they reveal? What patterns do you see in the data? Are there any individual observations that deviate from the overall pattern, and what do they reveal? For instance, in the java report, did the proportions differ when we compared the smokers to the non-smokers?
- Inferring from the data: What are valid statistical methods for drawing inferences "beyond" the data you collected? In the java study, is the 10%–15% reduction in hazard of death something that could have happened just by risk?
- Drawing conclusions: Based on what you learned from your information, what conclusions can you depict? Who do you lot think these conclusions utilise to? (Were the people in the coffee study older? Salubrious? Living in cities?) Tin you depict a cause-and-effect conclusion about your treatments? (Are scientists now saying that the coffee drinking is the cause of the decreased risk of death?)
Notice that the numerical assay ("crunching numbers" on the computer) comprises only a small part of overall statistical investigation. In this module, you will see how we tin answer some of these questions and what questions you should exist asking virtually any statistical investigation y'all read virtually.
Distributional Thinking
When data are nerveless to address a particular question, an of import first step is to recollect of meaningful means to organize and examine the data. The nearly fundamental principle of statistics is that information vary. The blueprint of that variation is crucial to capture and to understand. Often, conscientious presentation of the data will accost many of the research questions without requiring more sophisticated analyses. It may, however, point to additional questions that need to be examined in more detail.
Case i: Researchers investigated whether cancer pamphlets are written at an appropriate level to be read and understood past cancer patients (Brusk, Moriarty, & Cooley, 1995). Tests of reading ability were given to 63 patients. In addition, readability level was determined for a sample of thirty pamphlets, based on characteristics such as the lengths of words and sentences in the pamphlet. The results, reported in terms of grade levels, are displayed in Tabular array one.

These two variables reveal ii central aspects of statistical thinking:
- Data vary. More than specifically, values of a variable (such as reading level of a cancer patient or readability level of a cancer pamphlet) vary.
- Analyzing the pattern of variation, chosen the distribution of the variable, often reveals insights.
Addressing the research question of whether the cancer pamphlets are written at appropriate levels for the cancer patients requires comparing the two distributions. A naïve comparison might focus only on the centers of the distributions. Both medians plow out to exist ninth class, but because only medians ignores the variability and the overall distributions of these data. A more illuminating arroyo is to compare the entire distributions, for instance with a graph, as in Figure 1.
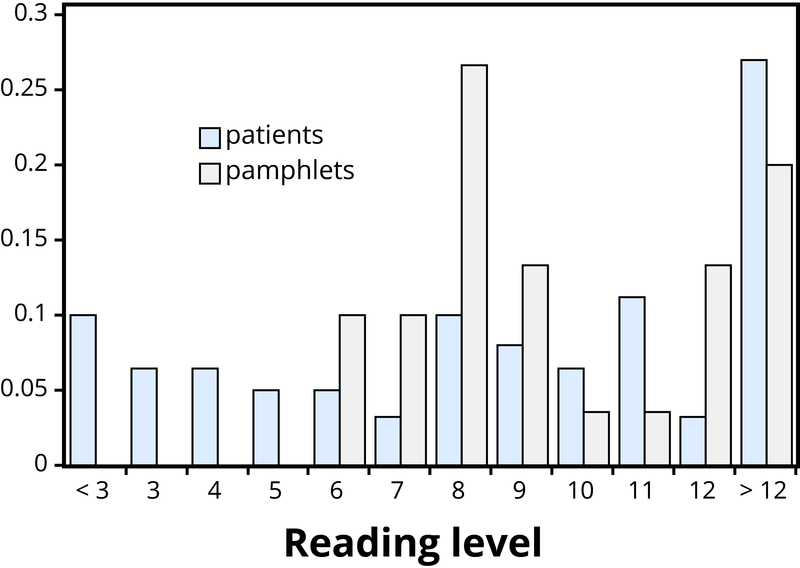
Effigy 1 makes clear that the 2 distributions are not well aligned at all. The most glaring discrepancy is that many patients (17/63, or 27%, to be precise) accept a reading level below that of the most readable pamphlet. These patients will need help to understand the data provided in the cancer pamphlets. Observe that this determination follows from because the distributions as a whole, non simply measures of heart or variability, and that the graph contrasts those distributions more than immediately than the frequency tables.
Statistical Significance
Even when nosotros find patterns in data, often there is nevertheless doubt in diverse aspects of the data. For example, in that location may be potential for measurement errors (even your own body temperature tin fluctuate by almost 1 °F over the course of the day). Or we may only have a "snapshot" of observations from a more than long-term process or only a small subset of individuals from the population of interest. In such cases, how can we determine whether patterns we see in our small gear up of data is convincing evidence of a systematic phenomenon in the larger process or population?
Case two: In a study reported in the Nov 2007 upshot of Nature, researchers investigated whether pre-verbal infants accept into account an individual's actions toward others in evaluating that individual as appealing or aversive (Hamlin, Wynn, & Bloom, 2007). In one component of the written report, 10-calendar month-old infants were shown a "climber" character (a piece of wood with "googly" eyes glued onto information technology) that could non get in up a hill in ii tries. Then the infants were shown ii scenarios for the climber's next try, one where the climber was pushed to the superlative of the hill by another graphic symbol ("helper"), and one where the climber was pushed back down the colina by another character ("hinderer"). The baby was alternately shown these two scenarios several times. And so the infant was presented with two pieces of wood (representing the helper and the hinderer characters) and asked to selection one to play with. The researchers found that of the 16 infants who made a clear pick, xiv chose to play with the helper toy.

One possible explanation for this clear majority effect is that the helping behavior of the one toy increases the infants' likelihood of choosing that toy. But are in that location other possible explanations? What virtually the color of the toy? Well, prior to collecting the data, the researchers bundled so that each color and shape (cherry square and blue circumvolve) would be seen by the aforementioned number of infants. Or perchance the infants had right-handed tendencies so picked whichever toy was closer to their correct paw? Well, prior to collecting the data, the researchers arranged information technology so half the infants saw the helper toy on the correct and half on the left. Or, maybe the shapes of these wooden characters (square, triangle, circle) had an effect? Perhaps, but again, the researchers controlled for this by rotating which shape was the helper toy, the hinderer toy, and the climber. When designing experiments, it is important to control for as many variables as might touch the responses every bit possible.
It is kickoff to appear that the researchers accounted for all the other plausible explanations. But there is one more than important consideration that cannot be controlled—if we did the study again with these sixteen infants, they might not brand the same choices. In other words, in that location is some randomness inherent in their selection procedure. Mayhap each infant had no genuine preference at all, and it was simply "random luck" that led to fourteen infants picking the helper toy. Although this random component cannot be controlled, we can apply a probability model to investigate the blueprint of results that would occur in the long run if random chance were the only factor.
If the infants were every bit likely to choice betwixt the two toys, then each infant had a l% chance of picking the helper toy. It'southward similar each babe tossed a coin, and if information technology landed heads, the infant picked the helper toy. So if nosotros tossed a money 16 times, could it land heads 14 times? Certain, it'southward possible, but it turns out to be very unlikely. Getting 14 (or more) heads in sixteen tosses is about as probable as tossing a coin and getting 9 heads in a row. This probability is referred to as a p-value. The p-value tells you lot how ofttimes a random process would requite a result at least as extreme as what was found in the bodily written report, assuming in that location was nothing other than random chance at play. So, if nosotros assume that each infant was choosing every bit, then the probability that 14 or more than out of 16 infants would choose the helper toy is found to exist 0.0021. Nosotros have but ii logical possibilities: either the infants take a genuine preference for the helper toy, or the infants have no preference (fifty/50) and an outcome that would occur only two times in 1,000 iterations happened in this study. Because this p-value of 0.0021 is quite small-scale, nosotros conclude that the report provides very strong evidence that these infants have a genuine preference for the helper toy. We often compare the p-value to some cutting-off value (called the level of significance, typically around 0.05). If the p-value is smaller than that cut-off value, then we reject the hypothesis that merely random chance was at play hither. In this case, these researchers would conclude that significantly more than than half of the infants in the written report chose the helper toy, giving strong evidence of a genuine preference for the toy with the helping behavior.
Generalizability

Ane limitation to the previous written report is that the conclusion but applies to the 16 infants in the study. Nosotros don't know much about how those 16 infants were selected. Suppose we want to select a subset of individuals (a sample) from a much larger grouping of individuals (the population) in such a fashion that conclusions from the sample tin can be generalized to the larger population. This is the question faced past pollsters every twenty-four hour period.
Example 3: The General Social Survey (GSS) is a survey on societal trends conducted every other twelvemonth in the United States. Based on a sample of nigh 2,000 adult Americans, researchers brand claims well-nigh what percentage of the U.Southward. population consider themselves to be "liberal," what pct consider themselves "happy," what percentage feel "rushed" in their daily lives, and many other issues. The fundamental to making these claims about the larger population of all American adults lies in how the sample is selected. The goal is to select a sample that is representative of the population, and a common style to achieve this goal is to select a random sample that gives every member of the population an equal chance of existence selected for the sample. In its simplest class, random sampling involves numbering every member of the population and then using a computer to randomly select the subset to be surveyed. About polls don't operate exactly like this, but they do apply probability-based sampling methods to select individuals from nationally representative panels.
In 2004, the GSS reported that 817 of 977 respondents (or 83.6%) indicated that they ever or sometimes experience rushed. This is a clear majority, but we over again need to consider variation due to random sampling. Fortunately, nosotros tin can use the aforementioned probability model we did in the previous example to investigate the probable size of this mistake. (Note, nosotros can use the money-tossing model when the actual population size is much, much larger than the sample size, as then we can nonetheless consider the probability to exist the same for every private in the sample.) This probability model predicts that the sample upshot will be within 3 per centum points of the population value (roughly 1 over the square root of the sample size, the margin of error). A statistician would conclude, with 95% confidence, that between fourscore.6% and 86.6% of all adult Americans in 2004 would accept responded that they sometimes or e'er experience rushed.
The key to the margin of error is that when we employ a probability sampling method, we tin brand claims nearly how often (in the long run, with repeated random sampling) the sample event would fall within a certain distance from the unknown population value past chance (pregnant by random sampling variation) alone. Conversely, non-random samples are oftentimes suspect to bias, meaning the sampling method systematically over-represents some segments of the population and under-represents others. We besides yet need to consider other sources of bias, such as individuals not responding honestly. These sources of fault are not measured past the margin of error.
Cause and Effect Conclusions
In many inquiry studies, the primary question of interest concerns differences between groups. Then the question becomes how were the groups formed (e.k., selecting people who already drink coffee vs. those who don't). In some studies, the researchers actively grade the groups themselves. But then we take a similar question—could any differences we observe in the groups exist an artifact of that group-germination process? Or mayhap the difference we observe in the groups is so large that we tin can discount a "fluke" in the group-germination procedure as a reasonable caption for what nosotros notice?
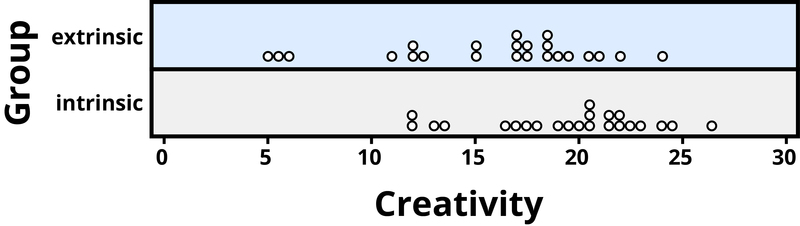
Example four: A psychology report investigated whether people tend to brandish more creativity when they are thinking about intrinsic or extrinsic motivations (Ramsey & Schafer, 2002, based on a study by Amabile, 1985). The subjects were 47 people with all-encompassing feel with creative writing. Subjects began by answering survey questions well-nigh either intrinsic motivations for writing (such as the pleasure of self-expression) or extrinsic motivations (such as public recognition). Then all subjects were instructed to write a haiku, and those poems were evaluated for inventiveness by a console of judges. The researchers conjectured beforehand that subjects who were thinking about intrinsic motivations would display more creativity than subjects who were thinking about extrinsic motivations. The creativity scores from the 47 subjects in this study are displayed in Figure 2, where higher scores signal more creativity.
In this case, the key question is whether the type of motivation affects creativity scores. In particular, exercise subjects who were asked about intrinsic motivations tend to take college inventiveness scores than subjects who were asked about extrinsic motivations?
Figure 2 reveals that both motivation groups saw considerable variability in creativity scores, and these scores accept considerable overlap between the groups. In other words, information technology's certainly not always the case that those with extrinsic motivations have higher creativity than those with intrinsic motivations, but there may still be a statistical tendency in this direction. (Psychologist Keith Stanovich (2013) refers to people'south difficulties with thinking about such probabilistic tendencies as "the Achilles heel of human being cognition.")
The mean inventiveness score is 19.88 for the intrinsic group, compared to 15.74 for the extrinsic grouping, which supports the researchers' conjecture. Yet comparing just the means of the two groups fails to consider the variability of creativity scores in the groups. We can measure out variability with statistics using, for instance, the standard divergence: v.25 for the extrinsic group and 4.40 for the intrinsic group. The standard deviations tell us that almost of the inventiveness scores are within about five points of the mean score in each group. Nosotros see that the hateful score for the intrinsic group lies within ane standard deviation of the mean score for extrinsic group. So, although at that place is a tendency for the creativity scores to exist college in the intrinsic group, on average, the difference is not extremely large.
We once more desire to consider possible explanations for this difference. The study only involved individuals with extensive artistic writing experience. Although this limits the population to which we tin can generalize, it does not explain why the mean creativity score was a bit larger for the intrinsic group than for the extrinsic group. Perchance women tend to receive higher creativity scores? Here is where nosotros demand to focus on how the individuals were assigned to the motivation groups. If only women were in the intrinsic motivation grouping and only men in the extrinsic group, then this would present a problem considering we wouldn't know if the intrinsic grouping did better considering of the different type of motivation or because they were women. However, the researchers guarded against such a trouble by randomly assigning the individuals to the motivation groups. Like flipping a coin, each individual was just as probable to be assigned to either type of motivation. Why is this helpful? Considering this random assignment tends to residue out all the variables related to creativity we can recall of, and even those nosotros don't retrieve of in advance, between the two groups. And then nosotros should have a similar male/female carve up between the two groups; we should have a like age distribution between the two groups; we should have a similar distribution of educational background between the 2 groups; and and then on. Random assignment should produce groups that are as similar every bit possible except for the type of motivation, which presumably eliminates all those other variables as possible explanations for the observed trend for college scores in the intrinsic group.
Only does this always work? No, then past "luck of the draw" the groups may exist a petty different prior to answering the motivation survey. Then then the question is, is information technology possible that an unlucky random assignment is responsible for the observed divergence in creativity scores betwixt the groups? In other words, suppose each private's verse form was going to get the aforementioned creativity score no matter which group they were assigned to, that the type of motivation in no fashion impacted their score. Then how often would the random-consignment process alone lead to a deviation in mean creativity scores as large (or larger) than 19.88 – 15.74 = iv.xiv points?
We once again want to apply to a probability model to approximate a p-value, merely this time the model will exist a scrap different. Think of writing everyone'southward creativity scores on an index card, shuffling up the index cards, then dealing out 23 to the extrinsic motivation grouping and 24 to the intrinsic motivation group, and finding the divergence in the group means. We (improve yet, the computer) tin can repeat this process over and over to see how frequently, when the scores don't change, random assignment leads to a difference in means at least equally large as 4.41. Figure 3 shows the results from ane,000 such hypothetical random assignments for these scores.
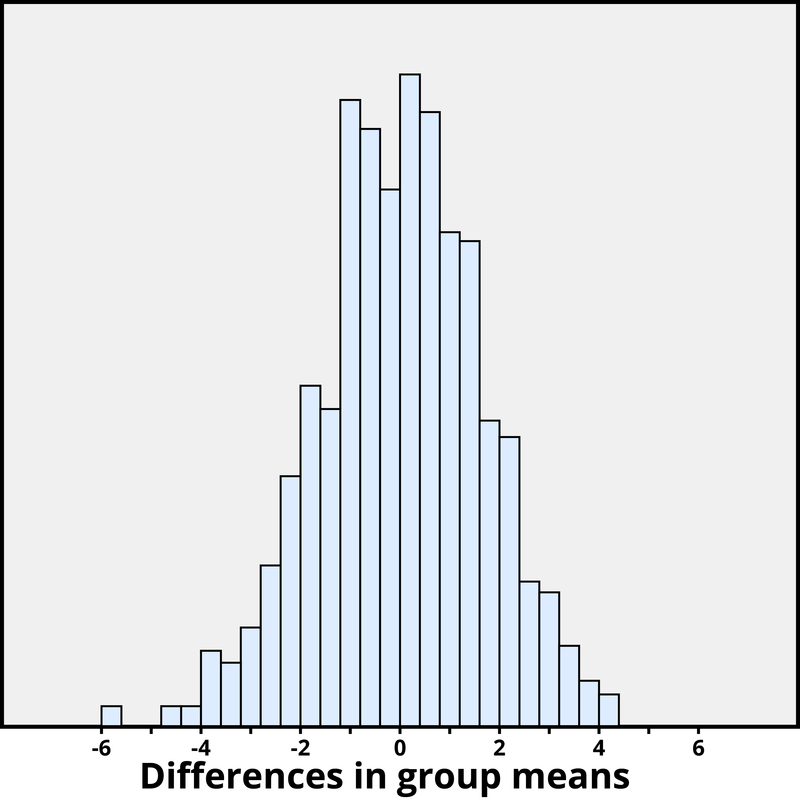
Just 2 of the i,000 simulated random assignments produced a difference in grouping means of 4.41 or larger. In other words, the guess p-value is 2/thou = 0.002. This small p-value indicates that information technology would be very surprising for the random assignment process lonely to produce such a big difference in group ways. Therefore, as with Case 2, we accept stiff show that focusing on intrinsic motivations tends to increase creativity scores, as compared to thinking about extrinsic motivations.
Notice that the previous statement implies a cause-and-effect human relationship betwixt motivation and inventiveness score; is such a strong conclusion justified? Yes, because of the random assignment used in the study. That should have balanced out whatsoever other variables between the two groups, and so now that the pocket-size p-value convinces us that the higher mean in the intrinsic group wasn't just a coincidence, the but reasonable explanation left is the difference in the blazon of motivation. Tin nosotros generalize this conclusion to everyone? Non necessarily—we could cautiously generalize this conclusion to individuals with all-encompassing feel in creative writing similar the individuals in this study, only we would still want to know more than about how these individuals were selected to participate.
Conclusion
Statistical thinking involves the conscientious blueprint of a written report to collect meaningful information to answer a focused research question, detailed assay of patterns in the data, and drawing conclusions that go across the observed data. Random sampling is paramount to generalizing results from our sample to a larger population, and random consignment is primal to drawing cause-and-effect conclusions. With both kinds of randomness, probability models help u.s.a. appraise how much random variation we tin can await in our results, in order to decide whether our results could happen by take chances alone and to estimate a margin of error.
So where does this exit us with regard to the coffee study mentioned at the offset of this module? We can answer many of the questions:
- This was a 14-yr study conducted by researchers at the National Cancer Constitute.
- The results were published in the June issue of the New England Journal of Medicine, a respected, peer-reviewed periodical.
- The written report reviewed coffee habits of more than than 402,000 people ages 50 to 71 from six states and two metropolitan areas. Those with cancer, centre disease, and stroke were excluded at the showtime of the study. Coffee consumption was assessed in one case at the commencement of the study.
- About 52,000 people died during the form of the report.
- People who drank between ii and five cups of coffee daily showed a lower risk also, merely the amount of reduction increased for those drinking six or more cups.
- The sample sizes were fairly big and and then the p-values are quite small-scale, even though percent reduction in risk was not extremely large (dropping from a 12% chance to well-nigh 10%–11%).
- Whether java was caffeinated or decaffeinated did not appear to impact the results.
- This was an observational study, so no cause-and-result conclusions can exist drawn between coffee drinking and increased longevity, contrary to the impression conveyed by many news headlines near this study. In particular, it's possible that those with chronic diseases don't tend to drink java.
This report needs to be reviewed in the larger context of similar studies and consistency of results across studies, with the abiding circumspection that this was not a randomized experiment. Whereas a statistical analysis tin nonetheless "accommodate" for other potential misreckoning variables, nosotros are not all the same convinced that researchers have identified them all or completely isolated why this decrease in decease gamble is axiomatic. Researchers tin can now take the findings of this written report and develop more than focused studies that address new questions.
Outside Resources
- Apps: Interactive web applets for pedagogy and learning statistics include the collection at
- http://world wide web.rossmanchance.com/applets/
- P-Value caricature
-
- Spider web: Inter-university Consortium for Political and Social Research
- http://world wide web.icpsr.umich.edu/index.html
- Web: The Consortium for the Advancement of Undergraduate Statistics
- https://www.causeweb.org/
Give-and-take Questions
- Find a recent research commodity in your field and reply the following: What was the main research question? How were individuals selected to participate in the written report? Were summary results provided? How strong is the bear witness presented in favor or against the research question? Was random assignment used? Summarize the main conclusions from the report, addressing the bug of statistical significance, statistical conviction, generalizability, and crusade and effect. Do you concur with the conclusions drawn from this study, based on the study design and the results presented?
- Is it reasonable to use a random sample of 1,000 individuals to draw conclusions about all U.S. adults? Explicate why or why non.
Vocabulary
- Crusade-and-issue
- Related to whether we say one variable is causing changes in the other variable, versus other variables that may be related to these two variables.
- Conviction interval
- An interval of plausible values for a population parameter; the interval of values within the margin of mistake of a statistic.
- Distribution
- The design of variation in data.
- Generalizability
- Related to whether the results from the sample can be generalized to a larger population.
- Margin of error
- The expected amount of random variation in a statistic; often defined for 95% conviction level.
- Parameter
- A numerical result summarizing a population (e.grand., hateful, proportion).
- Population
- A larger collection of individuals that we would like to generalize our results to.
- P-value
- The probability of observing a item outcome in a sample, or more extreme, under a conjecture most the larger population or process.
- Random assignment
- Using a probability-based method to divide a sample into handling groups.
- Random sampling
- Using a probability-based method to select a subset of individuals for the sample from the population.
- Sample
- The drove of individuals on which we collect data.
- Statistic
- A numerical result computed from a sample (east.g., mean, proportion).
- Statistical significance
- A result is statistically pregnant if it is unlikely to arise by chance alone.
References
- Amabile, T. (1985). Motivation and inventiveness: Effects of motivational orientation on artistic writers. Journal of Personality and Social Psychology, 48(2), 393–399.
- Freedman, N. D., Park, Y., Abnet, C. C., Hollenbeck, A. R., & Sinha, R. (2012). Clan of coffee drinking with total and cause-specific mortality. New England Journal of Medicine, 366, 1891–1904.
- Hamlin, J. K., Wynn, Thousand., & Blossom, P. (2007). Social evaluation by preverbal infants. Nature, 452(22), 557–560.
- Ramsey, F., & Schafer, D. (2002). The statistical sleuth: A form in methods of data analysis. Belmont, CA: Duxbury.
- Short, T., Moriarty, H., & Cooley, G. E. (1995). Readability of educational materials for patients with cancer. Periodical of Statistics Education, 3(2).
- Stanovich, One thousand. (2013). How to recollect straight most psychology (tenth ed.). Upper Saddle River, NJ: Pearson.
Authors
Artistic Eatables License



 Statistical Thinking past Beth Take a chance and Allan Rossman is licensed under a Artistic Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement.
Statistical Thinking past Beth Take a chance and Allan Rossman is licensed under a Artistic Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement. How to cite this Noba module using APA Fashion
Take chances, B. & Rossman, A. (2022). Statistical thinking. In R. Biswas-Diener & E. Diener (Eds), Noba textbook series: Psychology. Champaign, IL: DEF publishers. Retrieved from http://noba.to/ruaz6wjsSource: https://nobaproject.com/modules/statistical-thinking
0 Response to "An Example of Intrinsic Motivation Is Reading a Textbook Because"
Postar um comentário